Spin states: triplets and singlets

Spin States: Triplets and Singlets

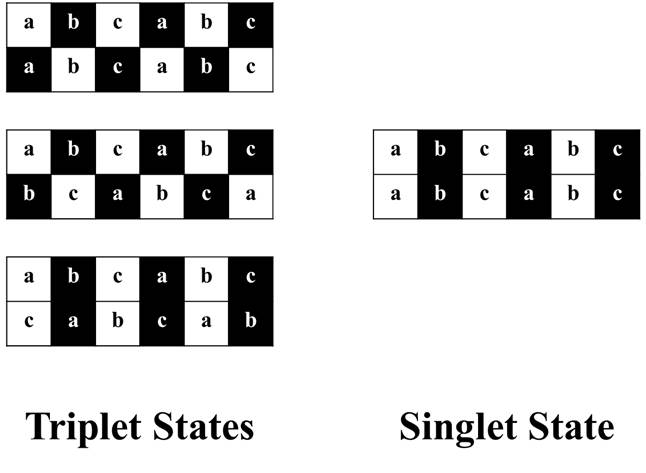
In quantum systems, such as two spin-½ particles (e.g., the two protons in a hydrogen molecule), the spin of each particle can be either “up” (↑) or “down” (↓). This results in four possible spin states:

  • (↑, ↑)
  • (↑, ↓)
  • (↓, ↑)
  • (↓, ↓)

Singlet and Triplet States

Within these four states, there is a key distinction:

  1. Singlet State: The spins are opposed, resulting in an antisymmetric state.
  2. Triplet States: The spins are aligned, forming three indistinguishable symmetric states.

Diagrams, such as those provided by the University of York Centre for Hyperpolarisation in Magnetic Resonance or Wikipedia, illustrate these states rigorously. Traditional quantum mechanics explains these states mathematically, based on the principle of an equation:

  • The difference between two objects that are the same is zero.

Chiralkine Counting: An Alternative Perspective

Chiralkine counting offers a novel viewpoint on singlet and triplet states, independent of equations. In this perspective:

  • “Up” (↑) and “Down” (↓) are mapped to “Same” and “Distinct.”
  • These labels oscillate interchangeably, guided by the logic gates XOR and XNOR, which represent mutually exclusive ways of drawing distinctions.

Visualizing the Relationships

The oscillation between same and distinct is easier to understand visually, such as through color-coded diagrams. These diagrams highlight the symmetry and cycling logic embedded in chiralkine counting.

Singlet State in Chiralkine Counting

In chiralkine counting, the singlet state is analogous to a scalar:

  • It represents the number of triplet states generated through counting.
  • For example, counting three objects (e.g., sheep) generates three copies of a triplet state. Counting two of those three copies produces two copies of another triplet state, leaving one behind, and so on.

This scalar property ensures that the singlet state is conserved through repeated counting.

Recursive NOT Gates and Oscillation

The singlet state corresponds to a recursive sequence of NOT gates:

  1. A NOT gate inverts its input:
    • If the input is True, the output is False, and vice versa.
  2. This recursive sequence forms a simple oscillation, where each NOT operation alternates the state generated by its predecessor.

Together, the NOT gates define the column for XOR and XNOR, placed one over the other. This sequence generates a simple oscillation, containing no triplets.

Triplet States and Logic Gates

In contrast, the triplet states correspond to the truth tables for the six logic gates:

  • XOR
  • XNOR
  • OR
  • AND
  • NOR
  • NAND

These gates represent the possible ways of coupling distinctions between “same” and “distinct,” demonstrating the rich structure inherent in chiralkine counting.

Conclusion

Chiralkine counting provides a fresh lens for understanding quantum spin states, replacing equation-based interpretations with a symmetrical, logic-driven process. By mapping spin states to logic gates, chiralkine counting reveals deeper connections between symmetry, oscillation, and distinction, offering new ways to explore quantum systems and their foundational principles.

(Acknowledgement: text drafted by Chat GPT based on a text I had drafted)