Counting objects: 1, 2, 3, etc., is amazing. You can count sheep (a) and record each one that has been counted by making a tally mark (b), then count the tally marks and record each one that has been counted by sliding a bead along a wire of an abacus (c). The number counted remains the same no matter how many times this is done or in what order each one is counted. Whenever an object is counted it is erased (/) from consideration and a new object recording the count is brought into consideration.
By way of example, here are four circles.
The circles are separated by crossings.
There are four crossings.
The order in which the circles are counted does not matter.
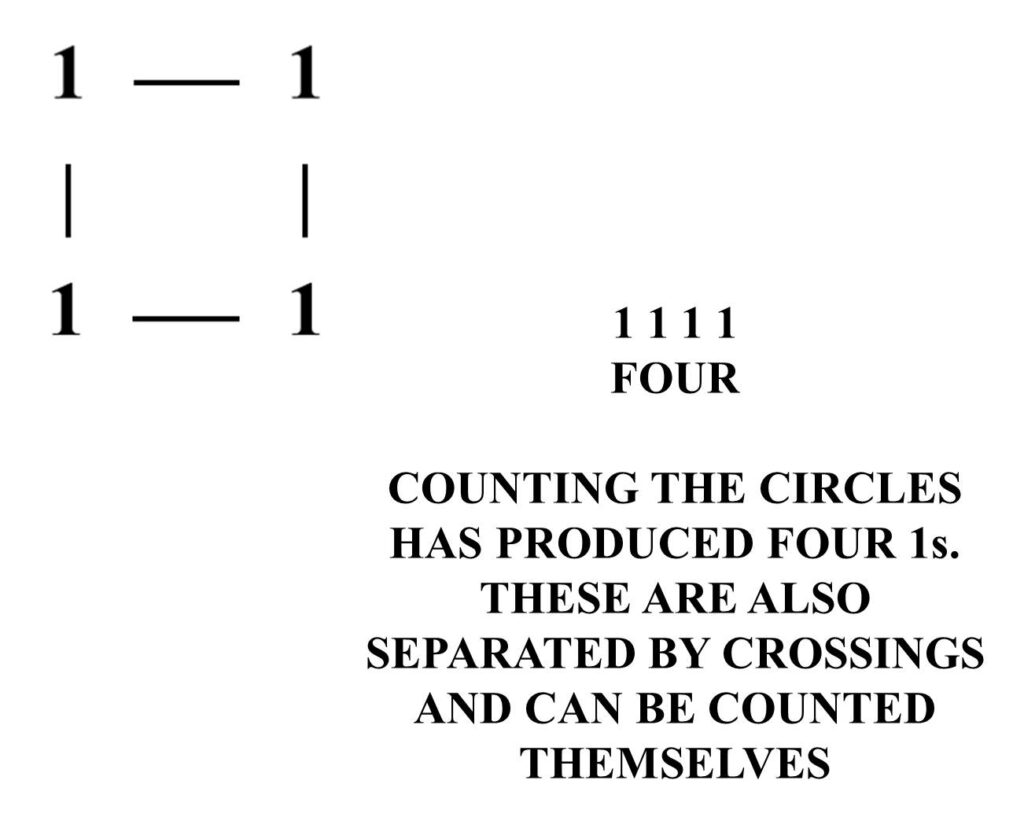
Each time a circle is counted, the circle and a crossing are cancelled out. A mark, 1, records that a circle has been counted.
The marks can be counted. Each is separated by a crossing.
The circles and marks are all objects. Counting them produces four more objects, and crossings.
We are taught to ignore the crossings when we count. They count as nothing (zero). This is where the problem with maths starts out. In chiralkine counting the crossings are just as important as the objects.