Chiralkine counting is controlled by dual logic.
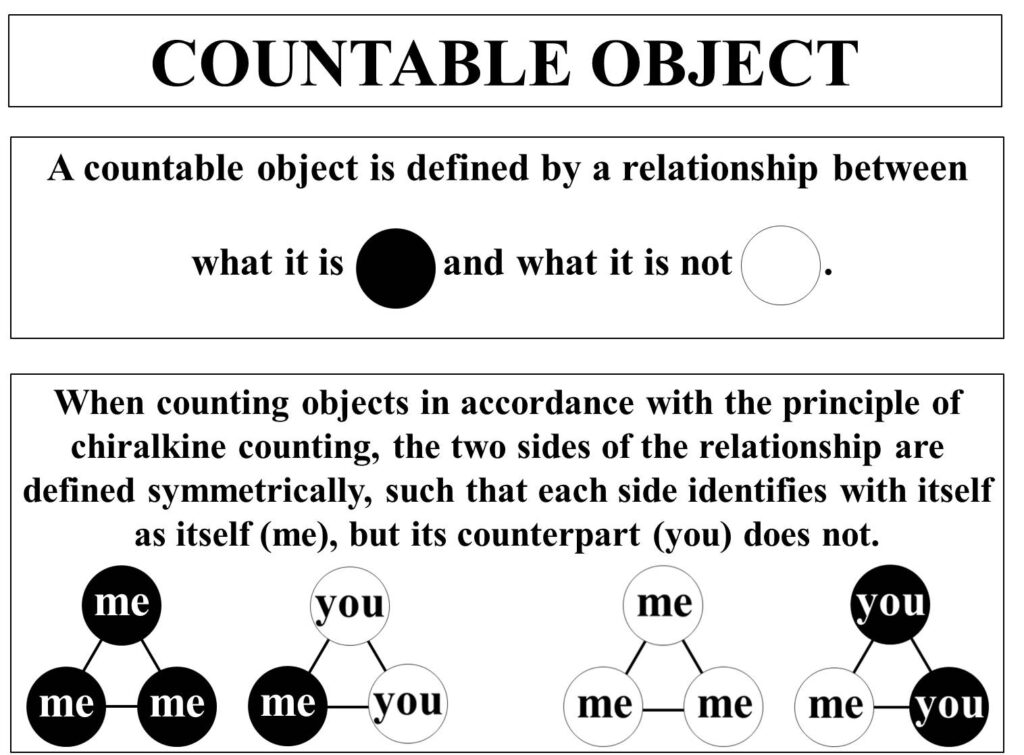
A countable object is defined by a relationship between what it is and what it is not, the two sides of this relationship being defined symmetrically, such that each is itself, not its counterpart.
Chiralkine counting is controlled by drawing and erasing distinctions in accordance with two mutually exclusive, mirror opposite logical operations. These operations are defined by the rules for the truth tables for the logic gates exclusive or (XOR) and not exclusive or (XNOR). Each of these compares two inputs and outputs a symbol defining whether the two inputs are the same or distinct. The symbols have mirror opposite meanings in the two tables. Together the tables treat the two sides of a relationship between is and not symmetrically.
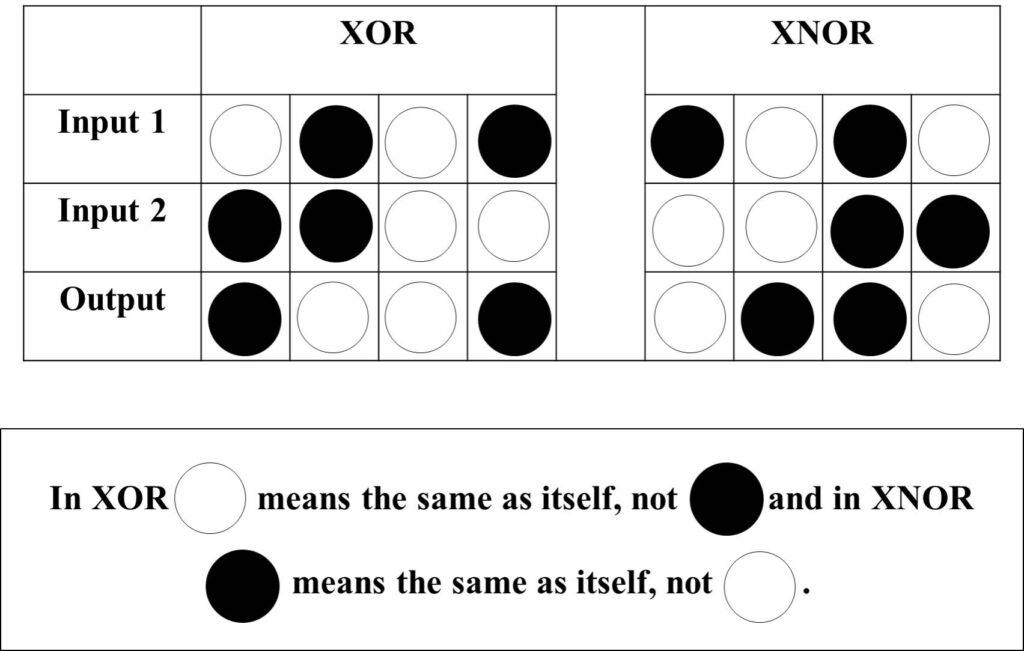
The order in which the two inputs are compared matters in chiralkine counting. Reversing the order switches the logic as between XOR and XNOR. As a result, a table of six rows is created that contains interpenetrating XOR and XNOR truth tables.
There are four different columns in a truth table. The four columns in the truth tables for XOR and XNOR are mutually exclusive, mirror opposites. Each pair of mirror opposite columns defines a relationship between what an object is and is not. There are six ways of ordering four objects in a ring. The truth tables for XOR and XNOR therefore interpenetrate in a six-membered cycle.
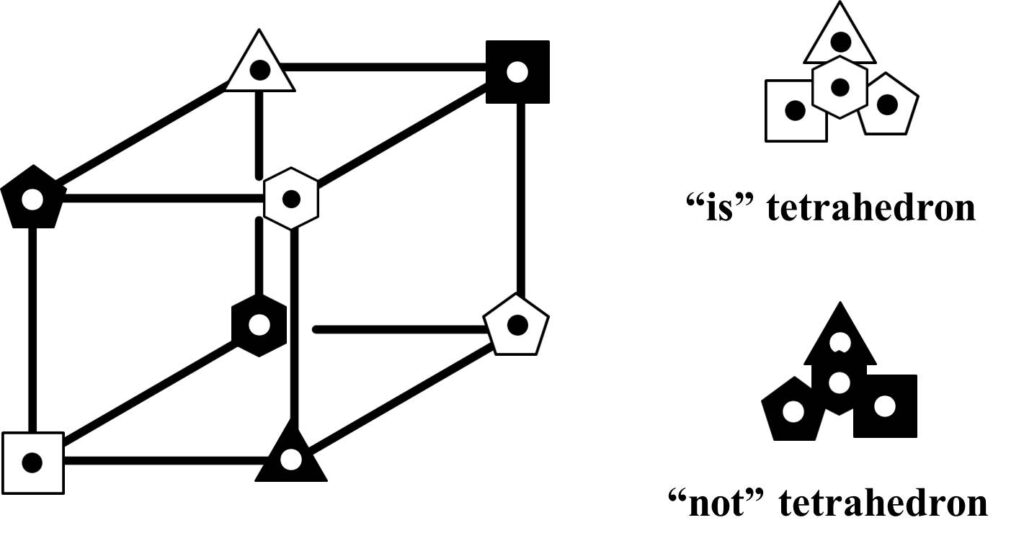
The permutation of four ordered objects, each defined by a relationship between what it is and what it is not, corresponds with rotation of 3D space. This can be modelled by the way in which the eight opposed corners of a cube, each representing a relationship between what an object is and is not, are permuted as the cube is rotated from one face to another. This is illustrated below. Opposed corners define a pair of chiral tetrahedrons of opposite sense (handedness), one tetrahedron mapping to “is” and the other to “not”. The name chiralkine was selected to allude to this handed (chiral) movement (kinetics).
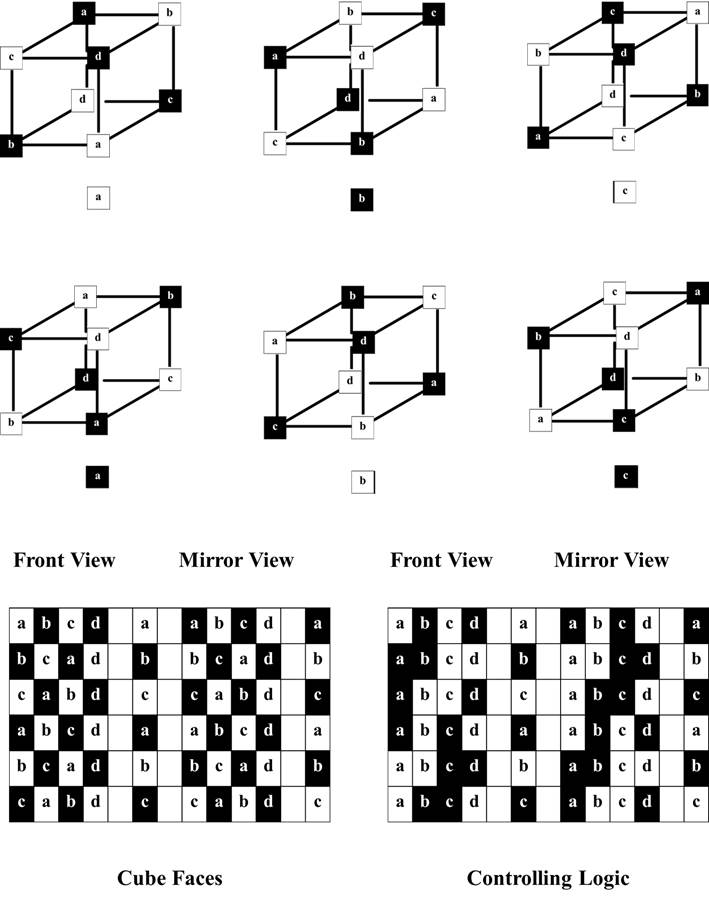
Instead of using different shapes to indicate four different objects, the letters a, b, c and d can be used. The advantage of doing this is that everyone remembers the order a, b, c, d.
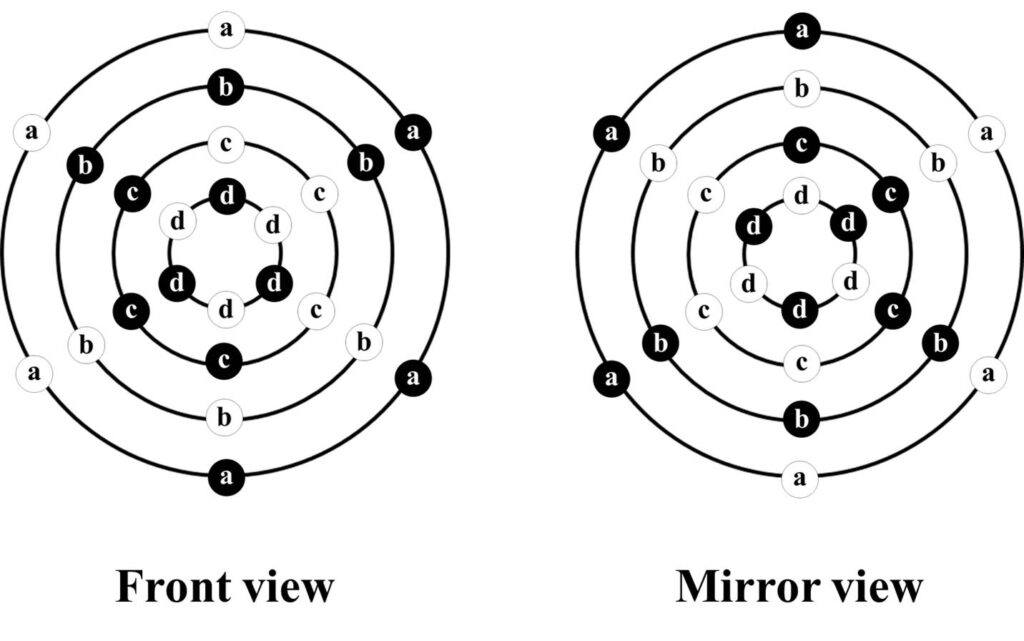
The cyclic interpenetrating nature of the controlling dual logic can be visualised easier by drawing the rows of truth table on concentric circles as shown below.
What appears to be the last of four ordered objects coding a cube face and generated by the controlling logic is actually related to the first object as not to is. There is duplication, which comes fundamentally from the way in which logic is controlled by chirality. Colour arises inherently from respecting mirror symmetry as the rules for the truth tables for the logic gates exclusive or (XOR) and not exclusive or (XNOR) are applied recursively. .
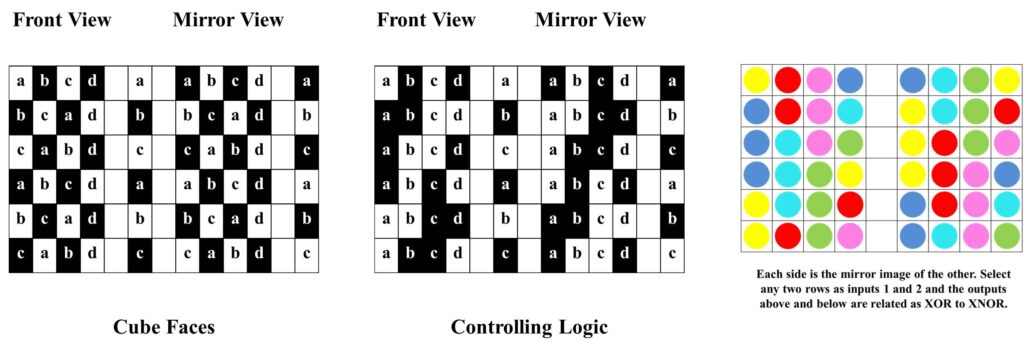
What appears to be a mirror pair of quaternions a,b,c,d generated simply by using XOR and XNOR symmetrically to draw a distinction between what is and what is not a countable object is actually a mirror pair of strings of six ordered objects, two of which are hidden. These mirror pairs of strings simply slide along through the cycle each time a counting step is performed.
Replacing the letters in the table with their colours, this looks like:
In effect, each of the comparisons black, white: white, white; white, black; and black, black, is being made twice, once according to the truth table for XOR and once according to the truth table for XNOR. Referring to the table for controlling logic above, each column d takes one each of the comparisons black, white and white, black, generating a simple black, white oscillation. Together they behave as NOT gates, which are simply inverters. The columns for a, b and c in the table take all other comparisons. Nevertheless, each of the columns for a, b, and c is also a simple black, white oscillation.
The members of each oppositional pair representing the is and not sides of a relationship defining an object: yellow/blue; red/cyan; magenta/green and black/white are related as the two sides of a coin, one side of which can be viewed directly and the other in a mirror.
The system is fractal, because the black/white centre controlled by the NOT function is actually the colour wheel rotated by 180 degrees, such that for each face (order of counting), the opposed colour is also that at the centre.
We have all been taught, wrongly, to count distinct objects once each. This incorrect way of counting is producing mounting social, economic, political and environmental problems. It has come about, because our languages and mathematics are constructed out of oppositions (black and white) in a way that privileges one side over the other.
We should be counting distinct objects twice each, once in respect of each side of black and white. We could then use these dual numbers to perform computation in a way that prevents one side of a relationship being privileged over the other. This would be a huge step towards solving many of the social, economic, political and environmental problems that we are facing. The way we think about relationships now is asymmetric, and that is the root cause.
A distinct object is defined by a relationship created by drawing a distinction between what it is and what it is not: an opposition (black and white). We have been taught to count only one side of this relationship (black). We call the other side of this relationship (white) nothing, and represent it with the symbol 0. This incorrect teaching causes us to privilege one side of our relationships over the other. We should be counting both, to ensure that the two sides of our relationships are treated symmetrically.
We incorrectly count each distinct object once only, in respect of what it is, because we assume erroneously that we can use either one of these two mutually exclusive ways of drawing distinctions without also using the other. This allows us to perform computation on the principle of equations and balance. For example, 1 is the same as 1, they balance, so 1-1 = 0.
The creation of countable money (+1) and debt (-1) out of uncountable balance (0) and independent return of countable (+1) and (-1) to uncountable balance (0) by spending the money and clearing the debt respectively is not possible in chiralkine counting. It takes three steps to switch between the countable (is) and uncountable (is not) sides of a relationship defining a countable object, which steps are controlled from both sides of the relationship, such that one side cannot complete the three steps without the other doing so as well.