Chiralkine counting is constructed mirror symmetrically from objects and processes defined relationally. Each is defined by mirror symmetric relationships between what it is and what it is not. These relationships are defined dynamically by drawing mirror symmetric distinctions between what an object is and what it is not. The process is dual and chiral (handed), hence the name chiralkine, derived from the Greek words for hand and movement.
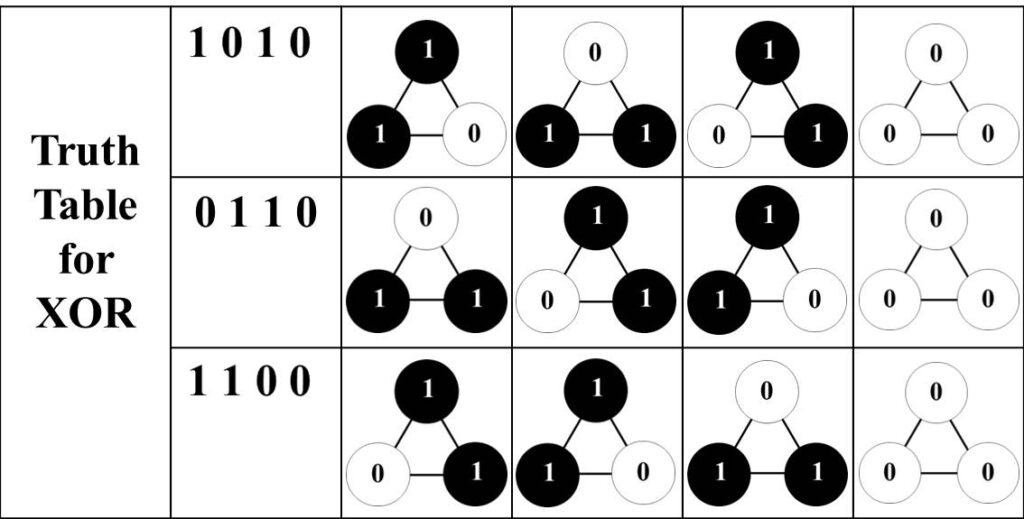
Each object and process has two sides, because distinctions are drawn using two mirror opposite processes, one defined by the truth table for logical XOR and one defined by the truth table for logical XNOR. When these two truth tables are placed side by side, the two mirror opposite processes for drawing distinctions appear to be mutually exclusive. This appearance is deceptive. It is a trap into which mankind has fallen, led by mathematicians intent on developing commutative, equation-based mathematics.
The truth tables for XOR and XNOR are interpreted dynamically, by comparing a symbol denoting a first input with a symbol denoting a second input to produce a symbol denoting an output. Reversing the order in which the inputs are compared produces the same output symbol. The process appears to be commutative. It appears that a comparison between the input symbols need be made only once. This is incorrect. It is incorrect, because the truth tables for XOR and XNOR are defined relationally. They interpenetrate one another. They are related through mirror symmetry – chirality – like left and right hands, the faces of a clock and the two enantiomers of a chiral molecule. There is a control mechanism hidden in plain sight.
The hidden control mechanism is anticommutative.
When one symbol is compared with another in the truth tables for XOR and XNOR, the output appears to be the same, regardless of the order in which the comparison is made. Indeed any two rows compared in any order will always generate the third. However, the symbols in a column behave like three corners of a ring (a triangle) that rotates whenever a comparison is made. The rotation is clockwise or anticlockwise, depending on order. However it does not appear to matter whether the ring is rotated clockwise or anticlockwise. Symmetry is conserved. The mechanism that conserves the symmetry is commutative.
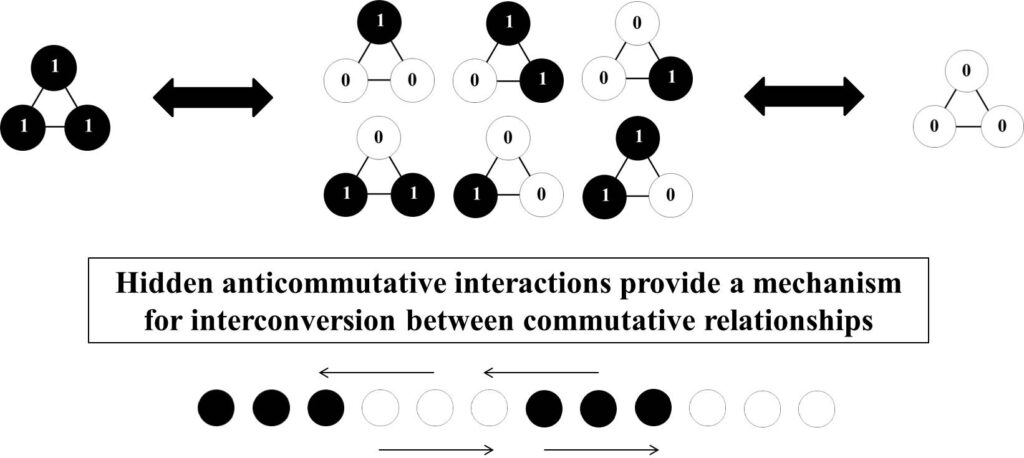
Commutative interactions create seemingly impenetrable walls. There is no commutative mechanism that enables interconversion of the rings: tunnelling between them. For each of XOR and XNOR there are two rings: for XOR: 0, 0, 0 and 1, 1, 0; and for XNOR: 1, 1, 1 and 0, 0, 1.
The mechanism that opens up the tunnels is anticommutativity. In a commutative interaction, there are actually two interactions, one from comparing first to second symbol and the other from comparing second to first symbol, but the output symbols are the same. In an anticommutative interaction, there are also two interactions, but the outputs are opposite. Clockwise and anticlockwise rotations produce opposite results. If the opposite logic is applied to any two corners of a ring defined in a truth table, it becomes a ring in the other truth table. For example, 0, 0, 0 can tunnel through to become 0, 0, 1 and 1, 1, 1 can tunnel through to become 1, 1, 0.
Conservation of mirror symmetry requires that all of the tunnelling is controlled as unitary transformations: all of the rings rotate synchronously. Hence when 0, 0, 0 tunnels through to become 0, 0, 1, another triangle 1, 0, 0 tunnels through to become 0, 0, 0. Putting all the commutative and anticommutative interactions together as required by conservation of mirror symmetry generates a cycle, which is the basis for how chiralkine counting works.