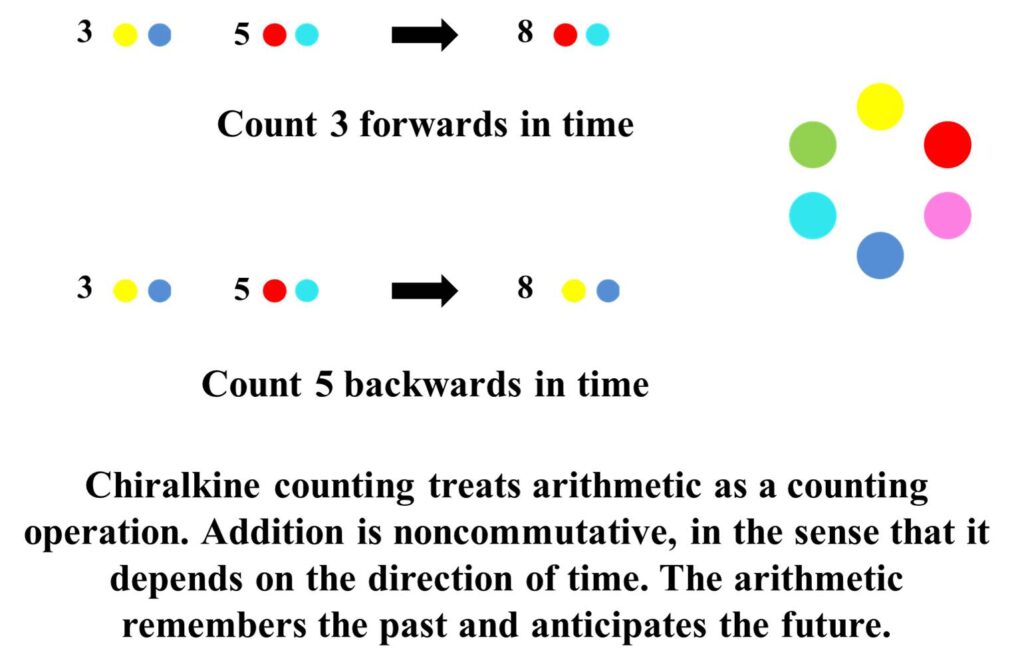
Arithmetic based on chiralkine counting treats all arithmetic operations as counting steps. Each step switches from one oppositional pair of colours to another in order around a chiralkine colour wheel. It can be forwards or backwards in time. The history is remembered and the future is anticipated.
When you think about it, the arithmetic we all use today is just one way of counting. When you count the quantity of distinct objects in a collection, you withdraw from consideration each distinct object after it has been counted and record this by bringing into consideration another distinct object. You subtract one from the quantity of distinct objects remaining to be counted and add one to the quantity of distinct objects that have been counted.
This arithmetic that we all use is based on the principle of an equation: the difference between two objects that are the same is nothing (zero). It constitutes a belief system. Like colour perception, it has no physical existence outside of our brains.
A number represents a quantity of distinct objects. When we add one number to another number in accordance with the principle of an equation, we produce just one number. This is inherent in the way equations work. We count across from one of the two quantities to the other. We ignore the withdrawal from consideration of the distinct objects that have been counted. When we perform subtraction we also produce just one number. However, we switch perception to the withdrawal from consideration of the distinct objects that have been counted. The distinct objects that have been subtracted disappear.
2 + 3 = 5 : 5 – 3 = 2 : 5 – (2 + 3) = 0 : 0 + (2 + 3) = 5 : 0 – 2 = 3 – 5
What happens to the 2 that are added to the 3? They become 0. What happens to the 3 that are subtracted from 5? They become 0.
Another characterising feature of arithmetic based on the principle of an equation is that positive and negative numbers can be created from nothing (zero). Each can be negated, independently, back to nothing (zero) in two steps. There is only one kind of nothing (zero). It is not a countable object. Again, this is inherent in the way that equations work.
Arithmetic operations based on chiralkine counting generate two numbers. There are two kinds of nothing (zero). They are both countable. Positive and negative numbers can be created from these two kinds of nothing (zero) and mutually negated back to these two kinds of nothing (zero) in three steps. One side cannot be negated back to a kind of nothing independently of the other. The three steps correspond with creation (from nothing), exchange and redemption (back to nothing). This is inherent in the way that chiralkine counting works, always looking from both sides of a relationship.
Think of the six states in a chiralkine counting cycle: a, b, c, a, b, c. Map a and a to two kinds of nothing (zero), (+0 and -0), b and b to one kind of pair of positive and negative integers (-1 and +1) and c and c to another kind of pair of positive and negative integers (+1 and -1).
–1 is turned by +1 into -0 and +1 is turned by -1 into +0
+1 is turned by -0 into +1 and -1 is turned by +0 into –1
.-0 is turned by +1 into -1 and +0 is turned by –1 into +1
Arithmetic based on the principle of an equation does not treat the two sides of a relationship symmetrically. Arithmetic based on chiralkine counting does.
For example, consider the addition of 2 to 3. Chiralkine arithmetic treats this as a counting operation. So it matters whether it is the 2 or the 3 that are being counted across to make up the 5. If it is the 2, then these are counted, this is recorded with the 3 and the 2 are withdrawn from consideration.
Putting this into a chiralkine counting cycle, the 2 can be coded as 2a and 2a. The 3 can be coded as 3b and 3b. Each of the 2a becomes 1b and each of the 2a becomes 1b. Now we have 5b and 5b. Note that in this operation we have also subtracted 2, because the 2 have been withdrawn from consideration.
For another example, consider the subtraction of 3 from 5. Again, chiralkine arithmetic treats this a counting operation, so 3 are being counting out from 5. They must be going somewhere else. We put this into a chiralkine counting cycle. The 5 can be coded as 5a and 5a. The subtraction of 3 from 5 is part of a counting operation that records 3b and 3b. This leaves 2a and 2a uncounted.
In chiralkine arithmetic the quantity of relationships defining what is and what is not a distinct object is conserved. What we think of as nothing (zero) is a perceptual construct (like colour) that our perception can switch into and out of. When our perception is switched into it, a quantity of relationships can be hidden.
In chiralkine arithmetic the two kinds or 0, +0 and -0 are countable, no different from the four kinds of 1 (+1, +1, -1, –1). The reason for drawing a distinction between them arises from their application in exchange. Think of selling me an object that is yours, not mine, so that it becomes not yours, mine. There is an inversion in the ownership. Chiralkine arithmetic can be used to couple that sale with other sales between each of us and third parties, such that each of us exchanges something we have to offer for something we want. In place of the concept of balance (zero) which banks and governments use in financial accounting, we can use the symbol +0 to represent a unit of quantity of what we have to offer (mine, not yours) and -0 to represent a unit of quantity of what we want (not mine, yours). Chiralkine arithmetic then takes us all through a chiralkine cycle of the four kinds of 1 (+1, +1, -1, –1) in place of credit (money) and debt used by banks and governments today.