Conventional counting works on the principle that a countable object is defined by a relationship created by drawing a distinction between what it is and what it is not, treating the two sides of this relationship asymmetrically, such that only the quantity on the “what it is” side of the relationship is recorded.
For example, consider four distinct objects.
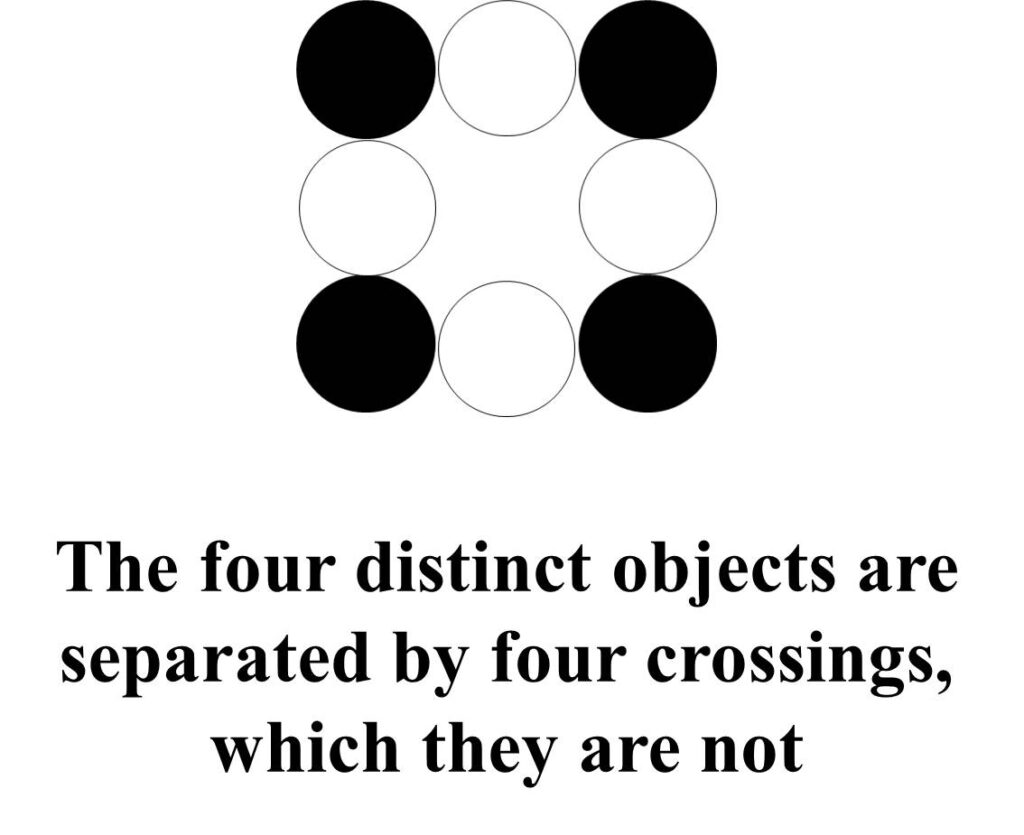
The four distinct objects are separated by crossings, which they are not.
The order in which objects are counted does not matter. For example, there are twenty four ways of ordering four distinct objects (4 x 3 x 2 x 1). These can be sorted into six rings of the four objects.
The four crossings that separate the four distinct objects are differently positioned in each case. Any path connecting the objects can be chosen: the crossings are delocalised. For this reason, it has become conventional wisdom that the crossings can be ignored. Four objects in a ring are treated as if they are in a chain, ignoring the crossing that separates the first counted object from the last.
Crossings, although part of the relationship drawing a distinction between what a countable object is and is not, are treated as uncountable in conventional counting. They are defined as the difference between two objects that are the same: nothing. This is a root cause of broken relationships between people and between mankind and the natural world.
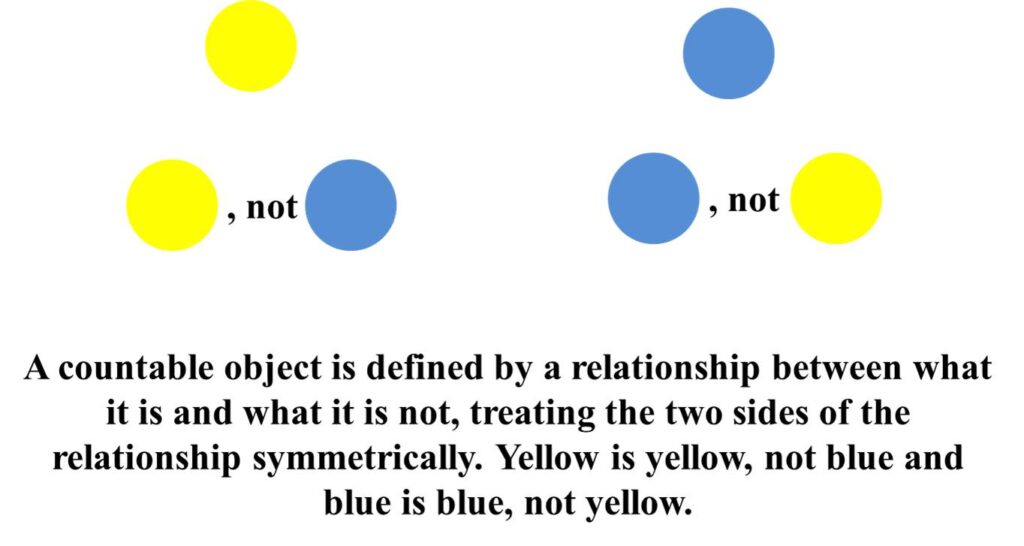
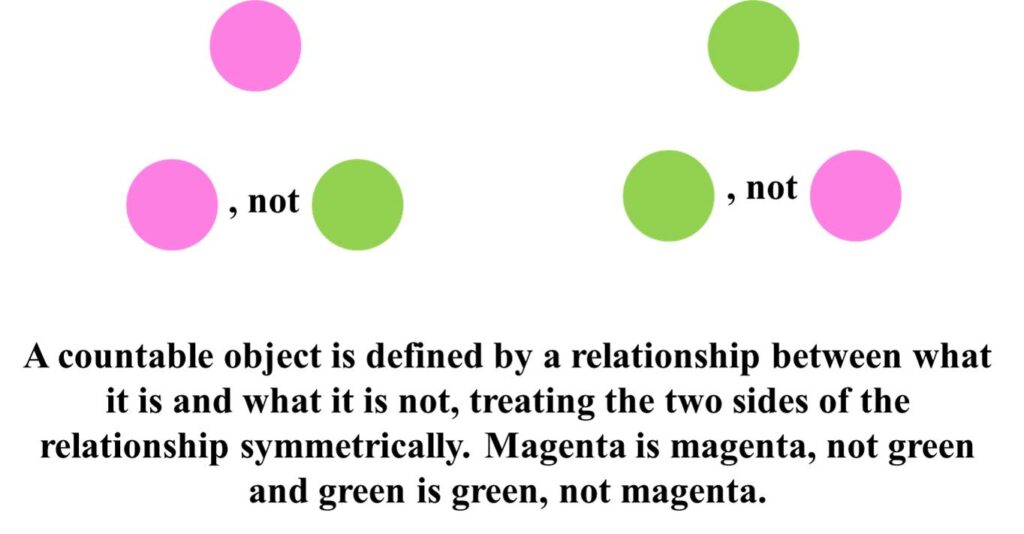
Chiralkine counting works on the principle that a countable object is defined by a relationship created by drawing a distinction between what it is and what it is not, treating the two sides of this relationship symmetrically. For example, the relationship between is and not can be as that between yellow and blue where yellow is treated as yellow, not blue and blue is treated as blue, not yellow, such that the two colours are treated symmetrically.
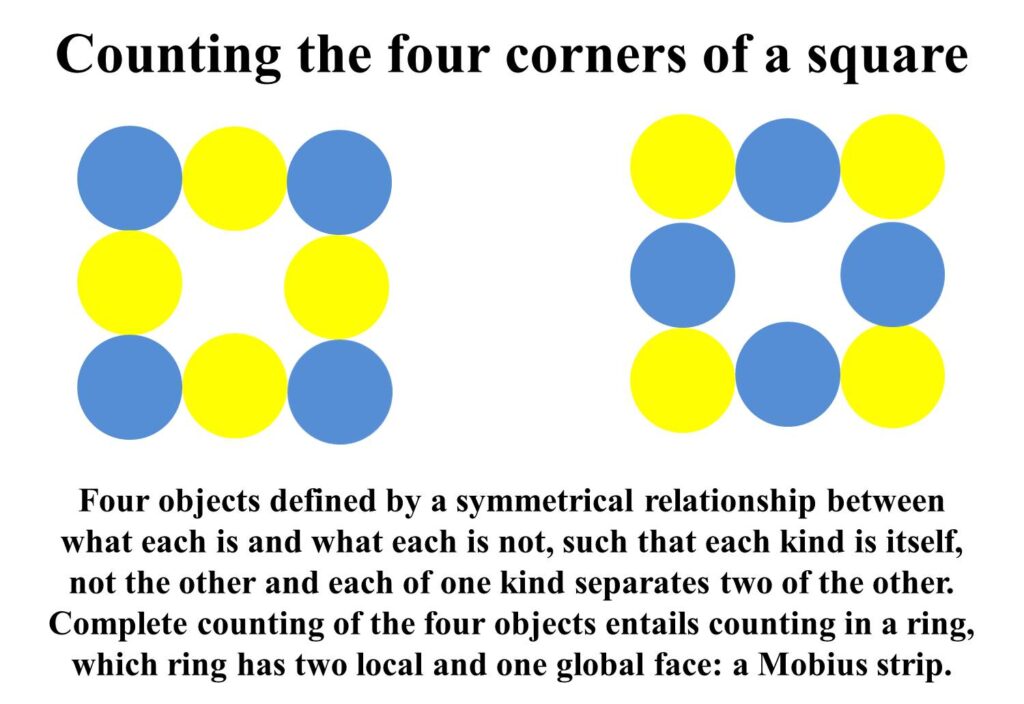
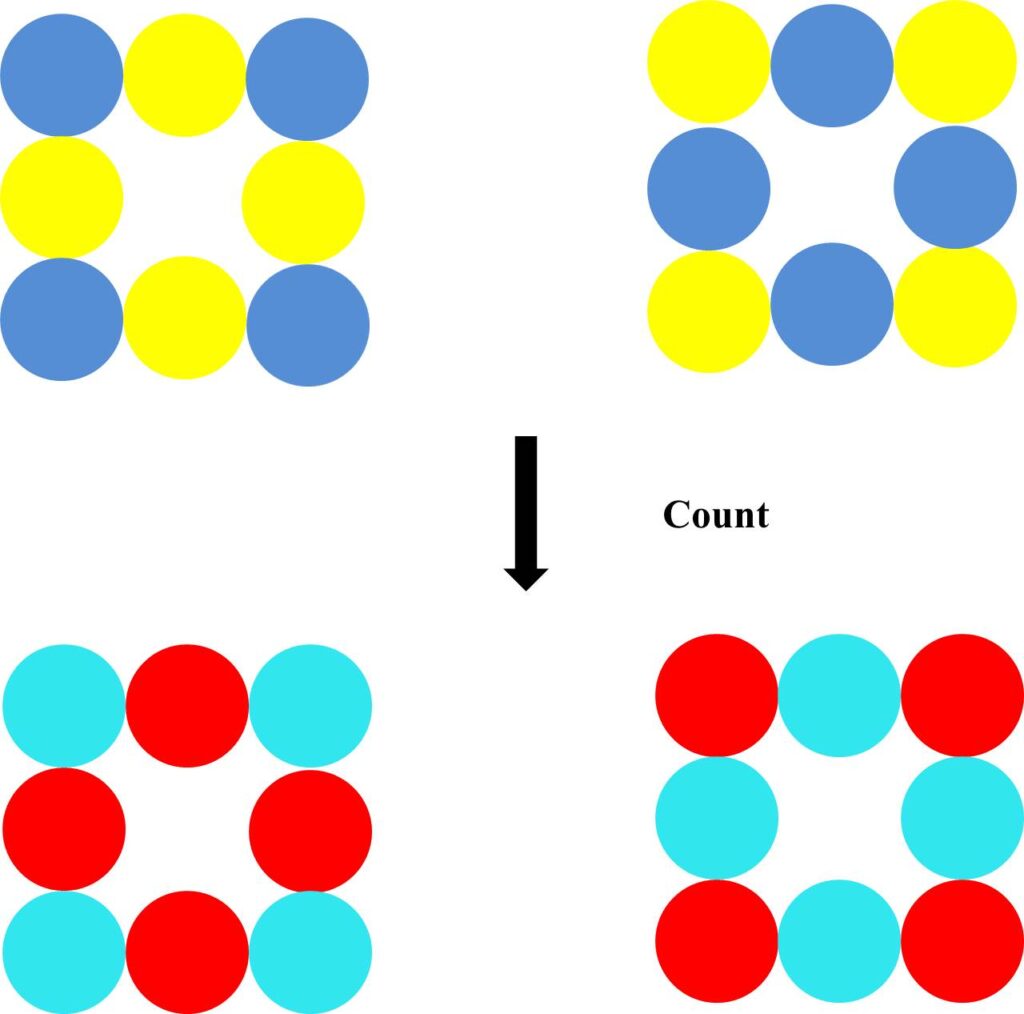
In a group of objects, each “is” and each “not” separates two of the other. There is an equal quantity of “is”s and “not”s in the group. The order of counting of the objects in the group does not matter, but complete counting requires that the objects are counted in a ring, such that no “is” or “not” is left unaccounted for. Hence, for example, counting the four corners of a square entails working through all of the four sides separating the corners.
Put another way, when an object is counted, the distinction creating the relationship that defines it is erased. Erasing the distinction withdraws the object from further consideration and so prevents double counting. The count is recorded as another countable object. For example, the distinction defining the relationship between yellow and blue is erased and the count is recorded by drawing a distinction defining a relationship between red and cyan.
For example, counting the four corners of the square as described above can be recorded as shown below.
The distinction defining the relationship between red and cyan can in turn be erased and the count recorded by drawing a distinction defining a relationship between magenta and green.
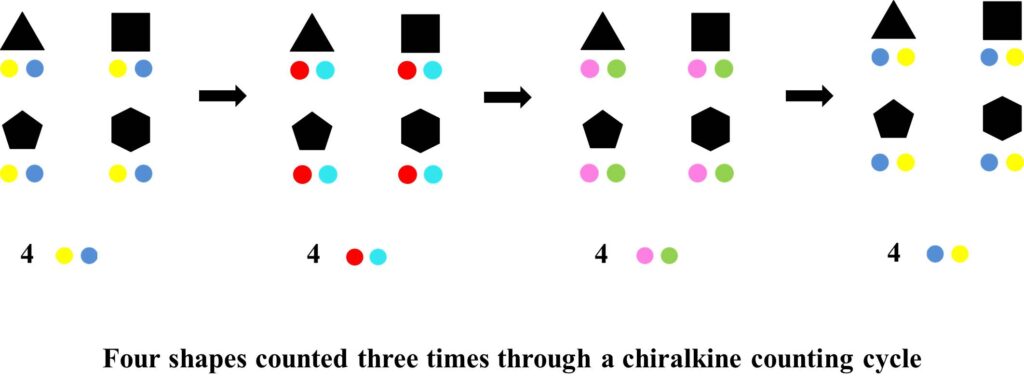
The repeated counting steps form a colour wheel. Three steps reverse the positions of the colours compared to their original positions. Six steps return the colours to their original positions.
Three counting steps reverses the positions of blue and yellow. This is illustrated below for four shapes as described above.
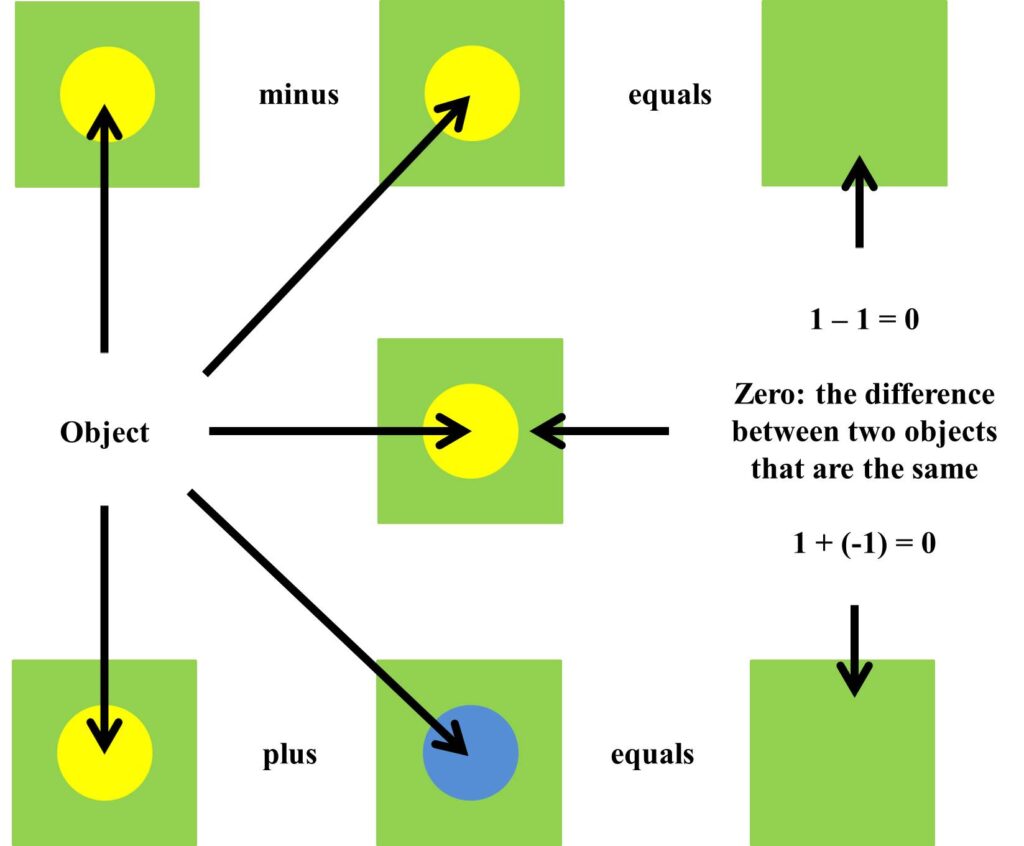
Note that the distinction between two opposed colours is erased by turning each into another colour in a pair, not by mixing them, which is the principle on which equations work (1 – 1 = 0). This principle is illustrated below using yellow, blue and green.